In this text, we will discuss the semi-empirical tricks that CFD codes use to model boundary layers based on their self-similarity. It is structured in three sections:

1. Boundary layer theory
2. Law of the Wall
3. Wall models
   • High Reynolds number models
   • Low Reynolds number models
4. Good meshing practices

Boundary layer theory

The formation of boundary layers near solid contours is a delicate issue for CFD modelers. In these regions, flow velocity and turbulence quantities vary abruptly in a non-linear way from zero on the wall surface (as imposed by the no-slip condition) their respective equilibrium freestream values, far away from the wall.

Despite their small dimensions, CFD models must treat boundary layers properly to obtain accurate results.

One may think that boundary layers, the flow region between a wall and the distance where $U \approx 0.99 U_\infty$, are insignificant due to their relatively small dimensions compared to an entire simulation domain. Nothing could be further from the truth. Treating boundary conditions in a proper way is necessary, as their effect on the flow behavior propagates far away from them:

• Boundary layers are sources of turbulence:

If you think about it, turbulence production occurs in large velocity gradients; i.e. when fluid layers flow at different velocities, they cause shear stresses that can trigger instabilities eventually large enough to make the flow transition from laminar to turbulent.

• Boundary layers damp turbulence quantities:

It may sound contradictory with the previous statement, but it’s not. As we approach solid contours, velocity tends to zero and, naturally, so do turbulence quantities. Also, this attenuation doesn’t varies from one direction to another, making turbulence no longer isotropic, hypothesis which most RANS models rely on.

So far, the importance of treating appropriately boundary layers in CFD models has been abundantly demonstrated, so a very fine mesh is needed to capture them, as we have seen that they’re characterized by very steep gradients of velocity and other flow variables. Remember that, in finite volume methods, each mesh cell can only hold a value of velocity, pressure, etc. and interpolation among adjacent cells is generally linear.

Think about it as if you took a photography portraying an object. In this case, you would also be discretizing a continuous reality (an image) into a discrete reality (a set of pixels). In this analogy, mesh cells would be pixels, which can only represent a single color. Don’t you think that it would make sense to increase the resolution in regions where there is more relevant information (e.g. within the object you want to portrait)? That would leave resolution relatively low in the background area, where colors seem to be more homogeneous or where you just don’t  care about what happens. That would make recording and treating the resulting image faster and the  file containing it sensitively smaller.

That is actually what some image compression algorithms do in photography and what we tend to do in CFD. In the latter case, instead of those extra pixels near the portrayed object, we would add extra layers of cells near the flow solid contours to capture appropriately boundary layers.

However, by doing so, two new issues will normally arise:

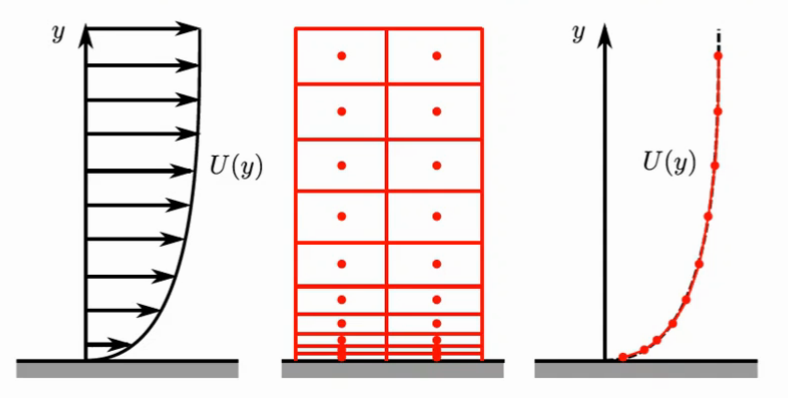
• Cells in this extra layer will have a huge aspect ratio.
• The total cell count will increase disproportionately.

Extreme aspect ratio values will reduce the mesh overall quality, eventually leading to certain problems of numerical nature. But the most immediate issue is that, as the total number of cells in the mesh increases, the computational requirements of our simulations will skyrocket: meshes will take longer to generate, we will require more powerful computers to run our simulations and the capacity to store them will become dramatically large.

Refining meshes to Resolve boundary layers down to the smallest scales may exert a critical effect on mesh quality and performance.

Now, the million dollar question is: is there any alternative to avoid this over-refinement, even if it involves a moderate sacrifice of accuracy?

To be more specific: can we replace all those extra cell layers in the wall vicinity by some numerical artifact capable of predicting the flow behavior in boundary layers? Can I know what non-linear profiles will be like before I run any simulation? Can I infer my boundary layer profiles out of measurements conducted on other boundary layers?

But the core question is: do boundary layers show self-similarity?

Good news: yes, they do!

Fortunately, conventional boundary layers show self-similarity, so variables accurately measured in one scenario can be extrapolated to others.

We will now discuss the semi-empirical strategies that CFD models use to model boundary layers based on their self-similarity. Each specific code features (probably many) of these approaches, but they can be split into two families:

• High Reynolds number models:

Appropriate for fully-developed turbulent flows without large pressure gradients and/or flow detachment. The RANS model equations are not modified. Instead, wall functions are applied to wall-adjacent cells.

High-Re models are computationally less demanding, but also less accurate than  low-Re models.

• Low Reynolds number models:

Appropriate for all kind of turbulent flows. No extra functions are added to the model. Instead, some parameters are introduced into the RANS equations to account for turbulence production and damping whose effect will only be appreciable in the near-wall region.

Low-Re models are computationally more demanding, but also more accurate than high-Re models.

Boundary layer theory is an extensive field of study within Fluid Mechanics. Readers interested in this topic are advised to use specific materials, such as Schlichting’s reference book [a].

Law of the Wall

Let us discuss briefly the self-similarity of boundary layers mentioned above, as that is the semi-empirical foundations which all wall models are based on in one way or another:

Back in the 1930s, a Hungarian mathematician named Theodore von Kármán put his finger on something that other contemporary scientists had been speculating about: that there were some common behavior patterns that repeated among apparently different boundary layers in a range of scenarios.

That led him to establish the so-called Law of the Wall based on the following non-dimensionalization of flow variables, such as velocity ($u$), and distance to the solid contour ($y$):

$u^+=\frac{u}{u_\tau}$

$y⁺ = y \frac{u_\tau}{\rho}$

Where $\rho$ is density and $u_\tau$ is the so-called shear velocity (a.k.a. friction velocity), a very useful variable with no physical meaning that represents the flow shear stress in velocity units:

$u_\tau = \sqrt{\frac{\tau}{\rho}}$

The shear velocity is generally 5% or 10% or the freestream velocity ($U_\infty$) and plays a very convenient role in wall treatment, as we cannot take the velocity on the wall as reference (remember that the no-slip condition imposes that $U_{y=0}=0$).

Remember that shear stress ($\tau$), the cornerstone of turbulence production, is proportional to the velocity gradient by a factor called viscosity ($\mu$):

$\tau = \mu \frac{du}{dy}$

Where $\mu$ is the fluid molecular viscosity.

These $⁺$ non-dimensional magnitudes and others that we’ll discuss later on are often referred to as “wall units” and are what makes extrapolation of the physical magnitudes among different boundary layers possible.

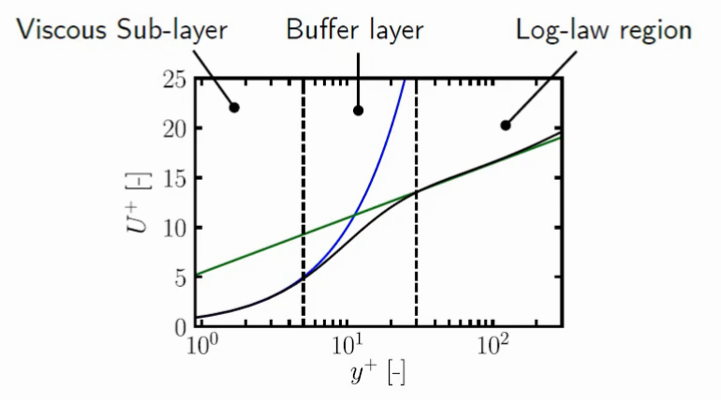
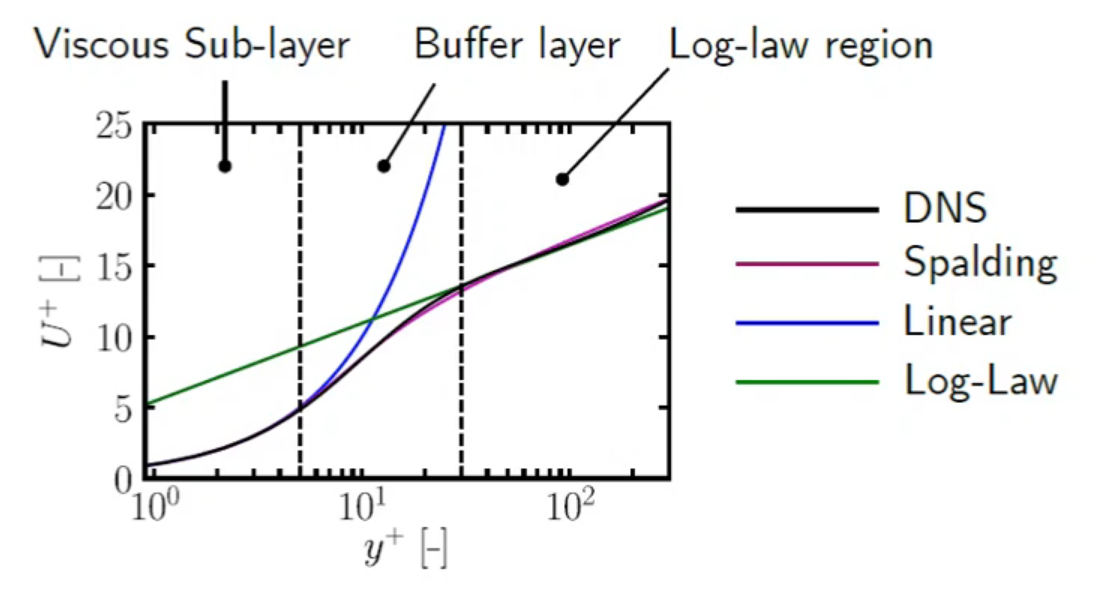
Fig. 2 shows the velocity profile in a boundary layer in wall units. Note that three sub-layers can be neatly identified, namely:

• Viscous sub-layer ($0<y^+<5$), near the wall, where viscous effects dominate the flow and the velocity profile is clearly linear:

$u^+ = y^+$

• Buffer sub-layer ($5<y^+<30$), in between sub-layers, where the velocity profile transitions from linear to logarithmic and no clear law can be observed:

$u^+ = ~ ?$

• Log-law sub-layer ($30<y^+<300$), where the velocity profile follows a log-law up to the end of the boundary layer:

$u^+ = \frac{1}{\kappa} \log{E y^+}+C^+$

Where $\kappa\approx 0.41$ is the von Kármán constant and $E\approx 9.8$, although both are empirical values that can vary from case to case. $C^+$ is also an empirical parameter and it changes according to the wall roughness (e.g. $C^+\approx 5$ in smooth walls).

The turbulent quantities derived from the Reynolds decomposition of the Navier-Stokes Equations ($-\overline{uv}$, $\nu_t$, $k$, $\varepsilon$, $\omega$, $l$, etc.) also show self-similarity and therefore they can also be non-dimensionalized as “wall units”:

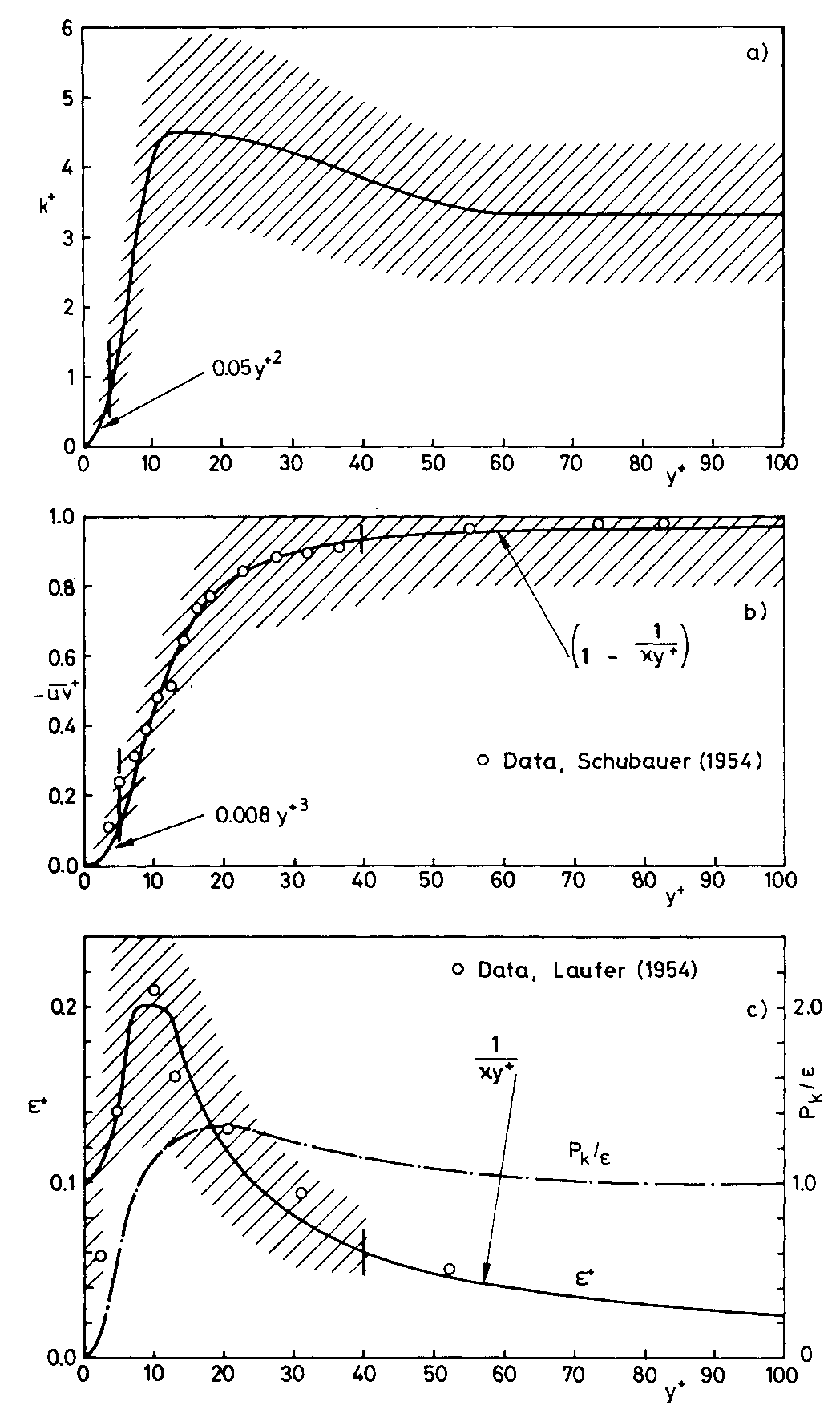
$\overline{uv}^+ = \frac{\overline{uv}}{u_\tau^2}$

$k^+ = \frac{k}{u_\tau^2}$

$\varepsilon^+ =\varepsilon \frac{\nu}{u_\tau^4}$

$\nu_t^+  = \nu_t \frac{\varepsilon}{k^2} $

Note that the term $\nu_t^+$ isn’t very common. Instead, the eddy viscosity in wall units is generally referred to as $C_\mu$.

Wall models

We can tell from Fig. 2 and 3 that the flow behavior near solid contours has nothing to do with the freestream conditions, so it’s only natural that conventional RANS models fail when predicting flow in this region.

However, knowing that we can extrapolate the profile shape of all flow magnitudes, as CFD modelers, we should wonder if we can take advantage of this fact. And that’s what wall functions do.

There are dozens of wall functions, but, as we saw above, they can be split into two families according to their approach, namely:

• High-Re functions
• Low-Re functions

High-Re models

High-Re wall functions use the Law of the Wall theory to reproduce what occurs between the wall and the wall-adjacent cell center.

The approach followed by High-Re wall functions is simple: they use the Law of the Wall theoretical formulation to add a set of equations that reproduce what occurs between the wall and the wall-adjacent cell center:

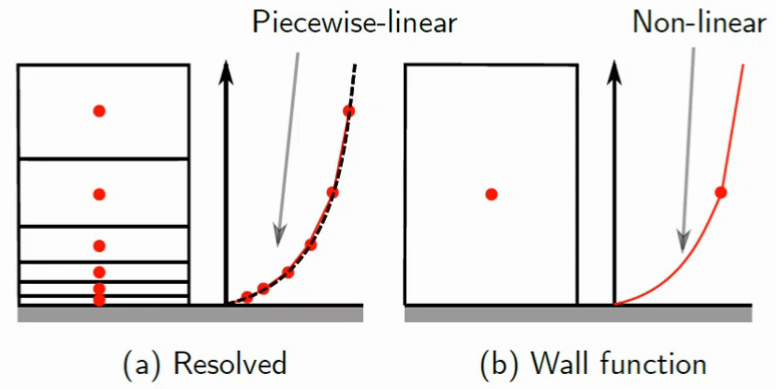
The saving of mesh resolution is obvious and CFD models switch from a linear profile to a logarithmic profile automatically, without any user input.

But what happens when the wall-adjacent cell center falls into the buffer region ($5<y^+<30$)? The easiest approach would be that the change between linear and log profile occurred at $y^+ = 11.25$, where both profiles intersect, but that would lead to non-negligible errors.

To overcome this issue, several approaches exist and each CFD code has its own why to combine or blend linear and logarithmic profiles. E.g., Spalding’s wall function uses a single (sensitively more complex) function for the entire boundary layer ($0<y^+<300$) which is always derivable and fits acceptably the actual velocity profile (see Fig. 5):

$y^+ = u^+ + 0.1108 [ e^{0.4u^+} – 1 – 0.4u^+ – \frac{1}{2}(0.4u^+)^2-\frac{1}{6}(0.4u^+)^3]$

But how does all this translate into CFD language? I.e. what do CFD codes actually do?

CFD codes need a single method to estimate the profiles of velocity and turbulence quantities applicable to all the wall-adjacent cells in a domain. What most of them do is something that will sound familiar if you understand how RANS model work: they use an effective or wall viscosity ($\nu_w$) which is the sum of a turbulence viscosity and the molecular viscosity:

$\nu_w = \nu + \nu_t$

The turbulence viscosity will obviously take zero value in the viscous sublayer and a non-zero value based on turbulence production derived from the velocity profile in the logarithmic region.

For an in-depth introduction to High-Re wall functions and wall functions in general, readers are strongly encouraged to watch this nice video from Fluid Mechanics 101 Youtube channel:

Low-Re models

Good meshing practices

References:

[1] Fluid Mechanics 101.

[2] von Kármán, Th. (1931), “Mechanical Similitude and Turbulence”, Tech. Mem. NACA, no. 611.

[3] Patel

[a] Schlichting